
今回は、度数の数え方を解説していきます。
前回の完全系と長短系の分類、長と短の分け方についての続きで、増(ぞう)と減(げん)、さらに重増(じゅうぞう)と重減(じゅうげん)について解説していきます。
前回の記事が基準となりますので、まだ読んでいない方はぜひ読んでみてください。
少し複雑になってきますが、順番に、わかりやすく丁寧にお伝えします。
増音程と減音程
度数の表し方には、
- 完全
- 長・短
- 増・減
- 重増・重減
というような種類がありましたね。
まずは完全系と長短系に分けることができました。
それぞれ以下のような分類です。
- 完全系…1・4・5・8度
- 長短系…2・3・6・7度
前回はここまで解説し、その完全系と長短系の度数から、
- さらに半音高いものを増音程
- さらに半音低いものを減音程
といいます。
それぞれの音程の度数からどのように変化しているのかを見て、度数の前に「増」や「減」を付けて表します。
次の項からそれぞれ具体的に見ていきましょう。
増
増音程について、完全系・長短系それぞれを見ていきましょう。
完全系の増
幹音同士の音程で、4度は多くの場合、全音2つと半音が1つの距離にありますが、ファからシを数えたとき、半音が含まれません。

これを増4度といいます。
次に変化記号がついた場合について、例を出して解説します。

ドからド#について見てみましょう。
まず、ドからドは同じ音同士なので1度ですね。
1度は完全系なので、ド#でここから半音高くなり増1度となります。

ドからソ#についても見てみましょう。
まず、幹音で考えてドからソは5度ですね。
5度は完全系で、ここからソ#で半音高くなり、増5度となります。
長短系の増
長短系の場合、増音程は長音程からさらに半音広がったものになります。
例を出しながら解説していきます。
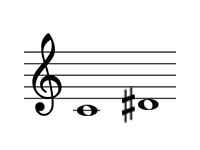
ドからレ#について見てみましょう。
まず、幹音で考えてドからレで2度ですね。
2度は長短系で、この場合は全音なので長2度です。
そしてシャープがついてさらに半音高くなっているので、増2度となります。
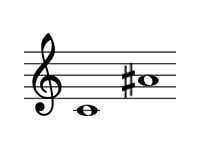
ドからラ#について見てみましょう。
まず、幹音間のドからラは6度ですね。
6度は長短系に分類され、この場合は全音が4つと半音が1つなので長6度です。
そしてラ#でさらに半音高くなっているため、増6度といいます。
減
増と同じように、完全系・長短系それぞれで解説していきます。
完全系の減
完全系の5度について見てみると、幹音間の音程の場合、ほとんどは全音3つと半音1つの距離にありますが、シからファだけ半音が2つ含まれます。

これを、減5度といいます。
変化記号がついた場合について例を見てみましょう。
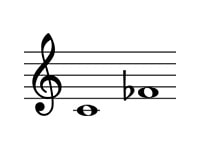
ドからファ♭について、まず、幹音のドからファで4度ですね。
4度は完全系で、さらにそこからファに♭がついて半音狭まっているので減4度となります。

ド#からオクターブ上のドについても見てみましょう。
まず、幹音のドからドで8度です。
8度は完全系で、さらにそこから下のドに#がついて半音狭まっているため、減8度となります。
ちなみに1度の音より狭まることはないので、1度に減音程はありません。
長短系の減
長短系の場合、減音程は短音程からさらに半音狭まったものになります。
長短系について例を出して解説していきます。

レからファ♭について見てみましょう。
まず、幹音のレからファで3度ですね。
3度は長短系に分類され、この場合全音1つと半音が1つ含まれるため、短3度です。
そしてファに♭でさらに半音狭まっているので、減3度となります。
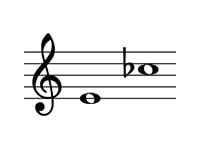
ミからド♭についても見てみましょう。
まず幹音で考えて、ミからドは6度です。
6度は長短系に分類され、この場合は全音3つと半音が2つ含まれているため短6度ですね。
そこからさらに、ドに♭がついていて半音狭まっているので、減6度となります。
完全1度・完全4度・完全5度・完全8度
増・減のない完全系の度数を、完全1度・完全4度・完全5度・完全8度といいます。
前回でも少し書きましたが、これらはとても協和性が高く、きれいな和音になります。
それぞれの音の周波数の比が1:1、3:4、2:3、1:2のようにきれいな数字となるのが特徴です。
ここで完全系についてまとめてみます。
- 同じ音同士の1度=完全1度
- 全音2つ半音1つの4度=完全4度
- 全音3つ半音1つの5度=完全5度
- 全音5つ半音2つの8度=完全8度
このようになります。
ここから半音高ければ増音程、半音低ければ減音程となります。
重増音程と重減音程
音程の表し方で、まだ重増・重減というものがありましたね。
これらについて解説していきます。
上記の増音程と減音程の度数から、
- さらに半音高いものを重増音程
- さらに半音低いものを重減音程
といいます。
度数の前に「重増」や「重減」を付けて表します。
だいぶややこしくなってきましたが、考え方は同じなのでそんなに難しく構える必要はありません。
次の項からそれぞれ具体的に見ていきましょう。
重増
重増音程は、増音程からさらに半音広がったものです。
1つ例を出して解説していきます。
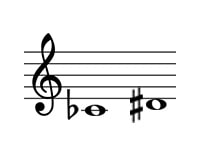
ド♭からレ#について見てみましょう。
幹音のドからレで2度、2度は長短系で、全音の2度は長2度でしたね。
レ#で半音広がっているため増2度となり、ここまでは増音程のところで出した例と同じです。
ここからさらに、ドに♭がついて音程が半音広がっていますね。
これが、重増2度となります。
重減
重減音程は、減音程からさらに半音狭まったものです。
こちらも1つ例を出します。
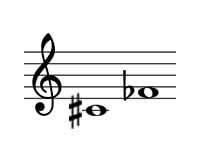
ド#からファ♭について見てみましょう。
まず幹音でドからファは4度です。
4度は完全系でした。
そしてファの♭で半音狭まり、減4度となります。
これも、減音程のところで出した例と同じです。
ここからさらにドに#がついているので、半音狭まり、重減4度となります。
音程の関係のまとめ
それぞれの音程についての関係を、図で表すと以下のようになります。
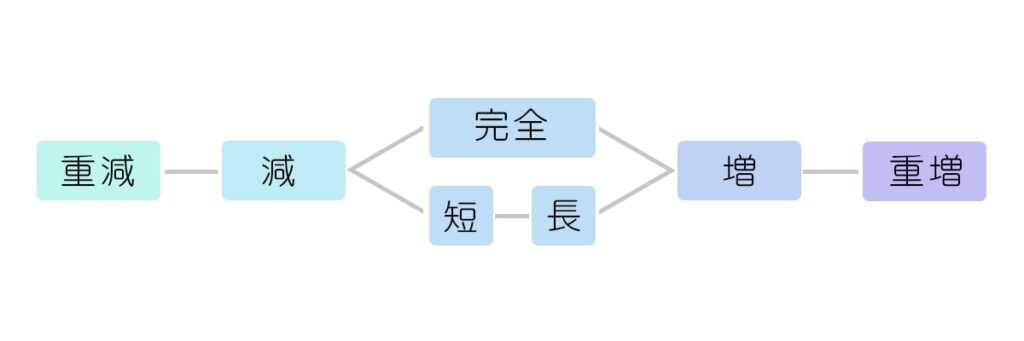
まずは完全系と長短系に分かれます。
完全系は半音狭まれば減音程、半音広がれば増音程となります。
長短系は同じ数字でも半音狭い方が短音程、広い方が長音程となり、短音程から半音狭まれば減音程に、長音程から半音広がれば増音程となります。
短音程から半音広がったものは長音程、逆に長音程から半音狭まったものは短音程という関係です。
そして、減音程からさらに半音狭まれば重減音程、増音程からさらに半音広がれば重増音程という感じになります。
まとめ
低い方の音を基準にしてその音からどれだけかということになります。
- 完全系・長音程からさらに半音広がると増音程
- 完全系・短音程からさらに半音狭まると減音程
- 増音程からさらに半音広がると重増音程
- 減音程からさらに半音狭まると重減音程







