今回は、度数による音程の分類について解説していきます。
完全1度、長2度などなどさまざまな音程が存在しますが、それらがどのように分けられるのかについて見ていきたいと思います。
また、分け方を決める振動数比についてもお伝えしていきますので、ぜひ読んでみてください。
- 音程の分類
- 振動数比
音程の分類
前回までで度数について詳しく書いてきましたが、音程は協和性によってそれぞれ分類分けされます。
協和性とは、音同士が響く調和の具合といったところで、どれだけ綺麗にハモるかということになります。
音程の分け方は以下の通りです。
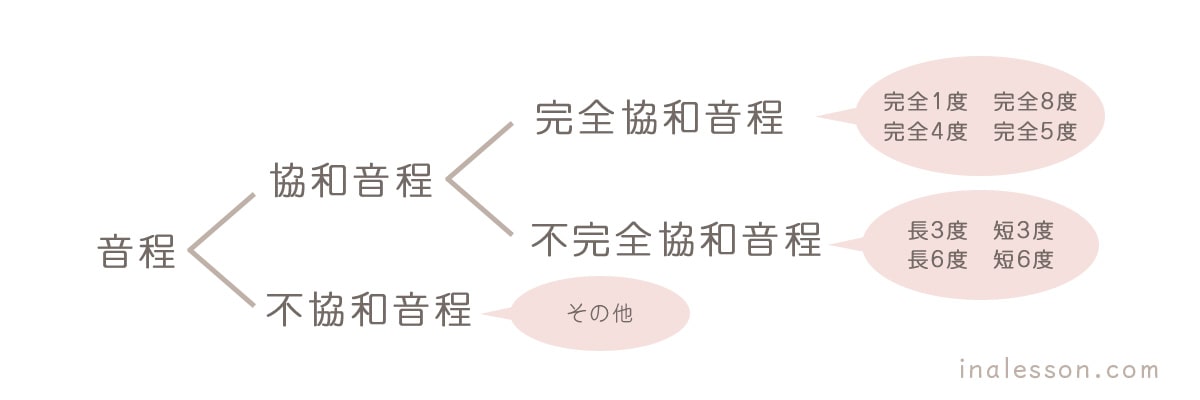
音程はまず、協和音程と不協和音程に分けられます。
協和音程には、完全1度・完全4度・完全5度・完全8度・長3度・短3度・長6度・短6度が属します。
その協和音程の中でも、完全1度・完全4度・完全5度・完全8度は完全協和音程、それ以外の長3度・短3度・長6度・短6度は不完全協和音程といいます。
下の表は協和音程のうちの分類です。
| 完全協和音程 | 不完全協和音程 |
|---|---|
| 完全1度 完全4度 完全5度 完全8度 | 長3度 短3度 長6度 短6度 |
そして協和音程以外の音程は、すべて不協和音程に属します。
それぞれについてもう少し詳しく特徴を見ていきましょう。
協和音程とは
協和音程は協和性の高いものが分類されます。
協和音程の中でも、完全協和音程と不完全協和音程の2つに分けられます。
完全協和音程
完全協和音程には、完全音程が属します。
例えば、完全1度は全く同じ音同士のことを言いましたね。
ユニゾンといったりします。
また、完全8度いわゆるオクターブのことです。
完全協和音程は、その名の通り協和性が特に高いことが特徴です。
とてもきれいにハモる音同士です。
ユニゾンやオクターブが協和性が高いというのはわかりやすいのではないでしょうか。
不完全協和音程
不完全音程には、長短3度・長短6度が属します。
完全協和音程ほどではなくとも、協和性が高い音程になります。
例えばドとミが長3度、ドとラが長6度ですね。
3度や6度はよく歌のハモリパートでも使われます。
安心するような感じの和音です。
不協和音程とは
協和音程以外の音程を、不協和音程といいます。
文字を見ると、協和性のない、調和しない和音という意味になります。
その名の通り、不協和音程は濁ったような響きがします。
全音階的音程でいうと、減5度や増4度もここに分類されます。
また、他の増音程や減音程、重増音程や重減音程、長短2度や長短7度はここに属します。
ですが、『綺麗』だとか『濁った』というのは人の感覚でもあり、人によって感じ方が違うかもしれませんね。
これにはきちんとした分け方があります。
その分け方というのを次の項から解説していきます。
協和性を決める”振動数比”
協和性が高いというのは綺麗にハモることと前述しましたが、これにはそれぞれの音の振動数が関係しています。
音は、空気を振動させる”波”です。
振動数とは、それぞれの音が同じ長さの時間で振動する波の数のことをいいます。
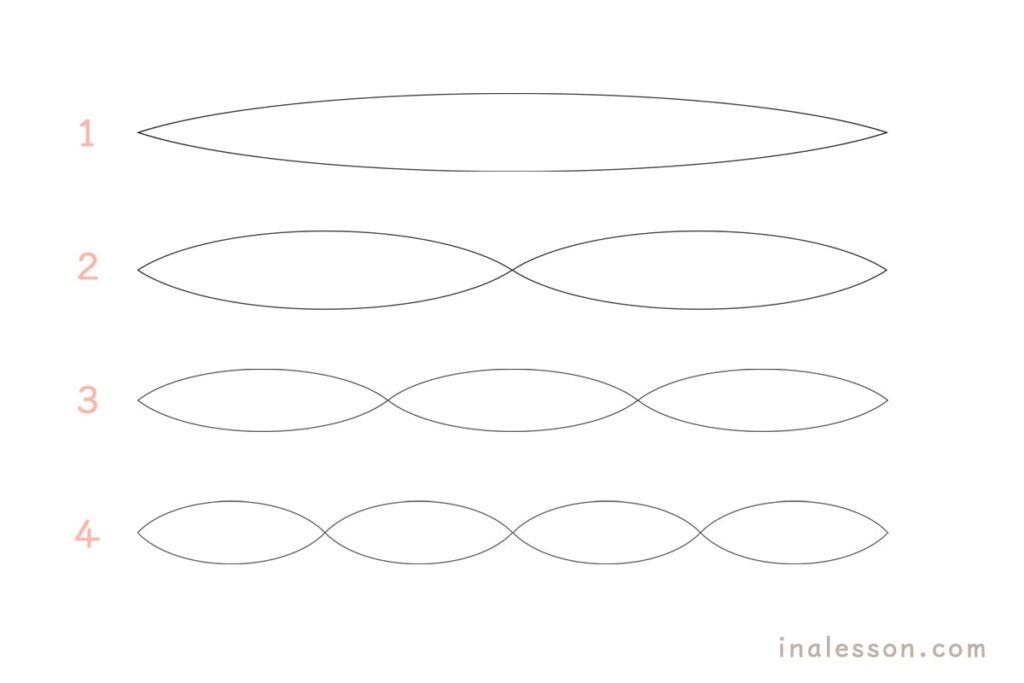
その振動数を比べてみた時に、比が1:2とか2:3とかきれいで簡単な整数の比になるものがハモっている音となります。
こういう整数の比で振動するそれぞれの音を倍音といいます。
振動数比が単純であるほど、協和性が高いとされます。
実際に、協和音程のそれぞれの振動数比を見てみましょう。
| 振動数比 | 音程 |
|---|---|
| 1:1 | 完全1度 |
| 1:2 | 完全8度 |
| 2:3 | 完全5度 |
| 3:4 | 完全4度 |
| 4:5 | 長3度 |
| 5:6 | 短3度 |
| 3:5 | 長6度 |
| 5:8 | 短6度 |
なかでも、完全1度と完全8度のことを絶対協和音程といいます。
振動数比を見てみると1:1、1:2と非常に協和性が高いです。
協和性の高い音程ほど、単純な数字になっていますね。
協和音程以外になると、例えば長2度は8:9となり、やはり振動数比は少し複雑な数字になってきます。
長2度というと、ドとレのような隣り合った全音で、確かに濁ったように感じますよね。
まとめ
実際に音を聴いてみると、協和性の違いが感じられるかと思います。
- 音程は協和性で分類される
- 振動数比がきれいで単純なほど協和性が高い
興味のある方はぜひ意識しながら音楽を楽しみましょう。








