今回は、広い音程の度数の問題を用意しました。
そのまま度数を数えても良いですが、今回では転回音程を用いて考えてみてください。
普通に答えを出すよりも早く導き出せます。
全部で12問です。
下に答えと解説がありますので、クリックして確認してください。
転回音程についてわからないという方は以下の記事を読んでみてください。
それでは早速出題していきます。
広い音程の度数
それぞれの音程を、転回音程を用いて考えてみてください。
第1問
ファ♭・ミ
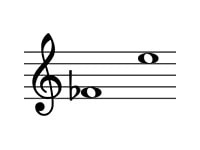
増7度
問題の転回音程は以下のようになります。
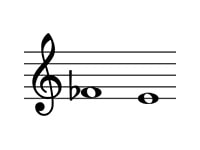
この音程は短2度からフラットによりさらに半音狭まった減2度です。
これを使って考えると、9-2=7 減⇔増なので問題の答えは増7度とわかります。
第2問
ミ#・レ♭
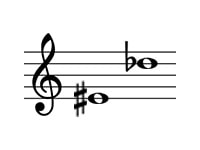
重減7度
問題の転回音程は以下のようになります。
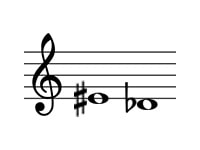
この音程は長2度からシャープとフラットによって半音2つ分広がった重増2度です。
これを使って考えると、9-2=7 重増⇔重減なので問題の答えは重減7度とわかります。
第3問
ファ#・レ

短6度
問題の転回音程は以下のようになります。

この音程は、短3度からシャープにより半音広がった長3度です。
これを使って考えると、9-3=6 長⇔短なので問題の答えは短6度とわかります。
第4問
ファ#・レ♭
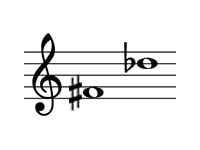
減6度
問題の転回音程は以下のようになります。
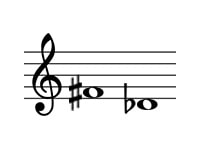
この音程は、短3度からシャープとフラットにより半音二つ広がった増3度です。
これを使って考えると、9-3=6 増⇔減なので問題の答えは減6度とわかります。
第5問
ソ#・ファ
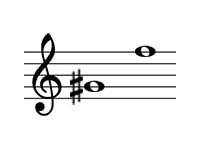
減7度
問題の転回音程は以下のようになります。
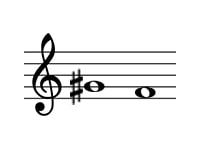
この音程は、長2度からシャープによって半音広がった増2度です。
これを使って考えると、9-2=7 増⇔減なので、問題の答えは減7度とわかります。
第6問
ド#・シ#
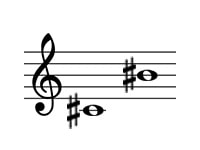
長7度
問題の転回音程は以下のようになります。

この音程は、短2度からシャープにより各音半音ずつ上がっているので変わらず短2度です。
これを使って考えると、9-2=7 短⇔長なので問題の答えは長7度とわかります。
第7問
ソ♭・ミ#
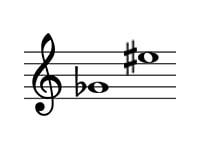
重増6度
問題の転回音程は以下のようになります。
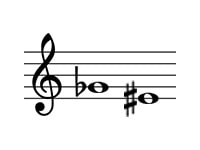
この音程は、短3度からシャープとフラットにより半音2つ分狭まった重減3度です。
これを使って考えると、9-3=6 重減⇔重増なので、問題の答えは重増6度とわかります。
第8問
ド・ラ#
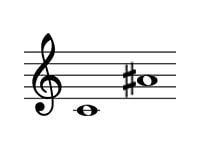
増6度
問題の転回音程は以下のようになります。
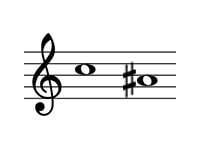
この音程は、短3度からシャープにより半音狭まった減3度です。
これを使って考えると、9-3=6 減⇔増なので、問題の答えは増6度とわかります。
第9問
ラ・ソ

短7度
問題の転回音程は以下のようになります。

この音程は長2度です。
これを使って考えると、9-2=7 長⇔短なので問題の答えは短7度となります。
第10問
ミ・ド♭

減6度
問題の転回音程は以下のようになります。
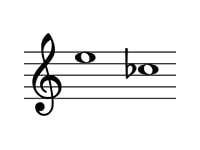
この音程は、長3度からフラットによりさらに半音広がった増3度です。
これを使って考えると、9-3=6 増⇔減なので、問題の答えは減6度とわかります。
第11問
レ・ド#
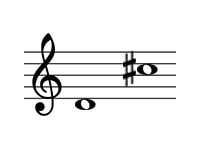
長7度
問題の転回音程は以下のようになります。
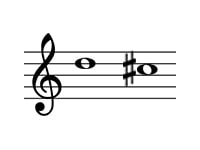
この音程は、長2度からシャープにより半音狭まった短2度です。
これを使って考えると、9-2=7 短⇔長なので問題の答えは長7度とわかります。
第12問
レ・シ♭

短6度
問題の転回音程は以下のようになります。
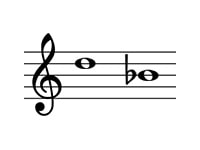
この音程は、短3度からフラットにより半音広がった長3度です。
これを使って考えると、9-3=6 長⇔短なので、問題の答えは短6度とわかります。

おつかれさま!できたかな!?
転回音程の使い方!
広い音程はパパっとわかりにくいですが、転回音程を使って考えるととてもわかりやすいです。
転回音程を考えて再度確認することで間違い防止にもなります。
知らなくても大丈夫ですが、便利ですね!
また、作曲などしてみたいという方は是非覚えておくと良いでしょう。








